RでIPTW法、Overlap weighting法を用いたKaplan-meier曲線を作成する

こんにちは、eURO2023です！

趣味（？）でRstudioをしています。

Kaplan-Meyer曲線について、前回お話しました。

応用編として、レトロスペクティブなデータ解析で有用なIPTW法を用いる機会があったので、備忘録としてまとめておきます。

更に、最近Overlap weighting法という重み付け法もあるようなので、合わせてまとめてみました！

Warning

私は統計については我流で学んでいます。

R、Rstudioについても我流です。

その点はご承知おきいただき、「統計素人がなんとなく統計やってみた」という目で観ていただければ幸いです。

質問、批評大歓迎です。

医師が統計を学ぶ上で、絶対読んだほうがよい！と思われる書籍を上げておきます。

今日から使える医療統計第2版

¥3,740 （2025/02/23 02:30時点 | Amazon調べ）

Amazon

楽天市場

ポチップ

いまさら誰にも聞けない医学統計の基礎のキソ第1巻まずは統計アレルギーを克服しよう! (Dr.あさいのこっそりマスターシリーズ)

¥3,080 （2025/02/23 02:30時点 | Amazon調べ）

Amazon

楽天市場

ポチップ

特に、新谷先生が執筆された「今日から使える医療統計」はおすすめです！

私は第一版を持っていますが、第二版が登場したようですね。

とても読みやすく、医療統計を始める上でも、論文の中身を理解する上でも非常に参考になります。

ある程度理解できるようになった今でも、よく読み返す本です。

「医療統計の基礎のキソ」は、更にわかりやすく、

「p値とはなにか？」

という超基本的な内容から、深く掘り下げてわかりやすく伝えてくれています！

第1巻から3巻までありますが、すぐに読めますよ。

下準備
応用編①：IPTW法によるKaplan-Meier曲線の作成
応用編②：Overlap weighting法によるKaplan-Meier曲線の作成
COX比例ハザードモデル
さいごに

下準備

今回も、前回作成した架空のデータシート”X”を用いていきます。

詳細は、下記ブログを参考にしてください。

RでKaplan-Meier曲線を描く方法

Rstudioを用いた、カプランマイヤー曲線の作り方を解説。

また、既存のCSVファイルやExcelファイルを読み込む場合は、readrパッケージやopenxlsxパッケージを用います。

一般的には、Rの解析にはExcelよりCSVの方が柔軟性があって良いらしいです。が、Excelファイルでもそんなに困ることは（私の場合）ありません。

# CSVファイルの読み込み
install.packages("readr")
library(readr)
X <- read_csv("絶対パス")

# Excelファイルの読み込み
install.packages("openxlsx")
library(openxlsx)
X <- read.xlsx("ファイルの絶対パス")

応用編①：IPTW法によるKaplan-Meier曲線の作成

IPTW法は、”Inverse Probability of Treatment Weighting”（逆確率重み付け法）法の略です。

観察研究において、治療群と対照群のバイアスを調整し、ランダム化試験に近い比較を行うための方法です。

観察研究では、治療を受けるかどうかはランダムに選ばれることはありません。

例えば、高齢者の方が特定の治療を受けやすい、重症患者がより積極的な治療を受ける、など様々なバイアスが実臨床では出てきます。

そのまま治療群と非治療群を比較すると、このようなバイアス、または交絡因子（年齢、性別、BMI など）が結果に影響してしまいます。観察研究が、ランダム化比較試験に比べて研究の質が落ちるとされているのは、このバイアスによる面が大きいと言われています。

IPTW 法を使うことで、治療の割り付けがランダム化されたかのようにデータを調整できると言われており、近年よく用いられるようになってきました。

さて、IPTW法を用いてKaplan-Meier曲線を作成するためのRスクリプトを確認しましょう。

★★2025年4月6日に、p値がIPTW法によるものを反映していなかったことが判明したので、Rスクリプトを大幅に更新しています★★

# 必要なパッケージを読み込み
library(tibble)
library(survival)
library(survminer)
library(brglm2)
library(survey)

# 欠損データの除去（complete cases）
X_complete <- X[complete.cases(X[, c("drug_A", "age", "sex","BMI",
                                     "Hb", "PS")]), ]

# Propensity Score (PS) モデルの構築
ps_model <- glm(drug_A ~ age + sex + BMI + Hb + PS,
                data = X_complete, family = binomial(), method="brglmFit")

# 傾向スコアによる予測値（確率）の取得
X_complete$ps <- predict(ps_model, type = "response")

# IPTW法の重み計算
X_complete$iptw_weight <- ifelse(X_complete$drug_A == 1, 
                                  1 / X_complete$ps, 
                                  1 / (1 - X_complete$ps))

# 重みの分布/NA除去
summary(X_complete$iptw_weight)
X_complete <- X_complete[!is.na(X_complete$iptw_weight), ]

# 重み付きサンプルデザイン（svydesign）
design <- svydesign(ids = ~1, weights = ~iptw_weight, data = X_complete)

# Kaplan-Meier推定とlog-rank検定（重み付き）
svykm_obj <- svykm(Surv(survival_month, survival) ~ drug_A, design=design)
svylogrank(Surv(survival_month, survival) ~ drug_A, design=design)

# survfitを使ったKaplan-Meier作図用オブジェクト
km_fit_iptw <- survfit(Surv(survival_month, survival) ~ drug_A, 
                       weights = iptw_weight, data = X_complete)

# p値の抽出とテキスト化
logrank_test <- svylogrank(Surv(survival_month, survival) ~ drug_A, design=design)
p_value <- as.numeric(logrank_test[[2]]["p"])
p_text <- paste0("p = ", signif(p_value, 3))

# IPTW法によるKaplan-Meier曲線の描画
ggsurvplot(
  km_fit_iptw, 
  conf.int = TRUE,
  risk.table = TRUE,
  title = "Kaplan-Meier Curve (IPTW adjusted)",
  legend.labs = c("No drug A", "Drug A"),
  xlab = "Time (months)",
  ylab = "Recurrent Probability",
  palette = c("#FC4E07", "#756BB1"),
  break.time.by = 12,
  pval = p_text
)

欠損データの除去（complete cases）

# 欠損データの除去（complete cases）
X_complete <- X[complete.cases(X[, c("drug_A", "age", "sex","BMI",
                                     "Hb", "PS")]), ]

complete.cases() は、その行にNAが含まれていなければTRUE、含まれていればFALSEを返します。

つまり、complete.cases(X[, ...]) で「6つの変数すべてにNAがない行」だけがTRUEになります。

X[...] で、TRUE になった行番号のデータだけを取り出して、X_complete に代入しています。

この処理で、「drug_A, age, sex, BMI, Hb, PS に1つでもNAがある行は除き、残った行だけを新たなデータフレーム X_complete に保存」します。

この作業は、後にsvydesign() を用いるために行っています。

svydesign()は、 weights に欠損値 (NA) が含まれているとエラーが出てしまうからです。

Propensity Score (PS) モデルの構築

# Propensity Score (PS) モデルの構築
ps_model <- glm(drug_A ~ age + sex + BMI + Hb + PS,
                data = X_complete, family = binomial(), method="brglmFit")

glm() は一般化線形モデル（Generalized Linear Model, GLM）を作成する関数です。

glm()は、Rの基本的なパッケージに含まれているので、インストールやlibrary()の必要はありません！

drug_A ：目的変数。「薬Aを投与されたか（1: はい, 0: いいえ）」を表す二値変数（binary変数）。

age + sex + BMI + Hb + PS ：説明変数。drug_A を予測するための要因（年齢、性別、BMI、ヘモグロビン値、PS）を入力する。

data = X ：使用するデータフレームとして、X を指定。

family = binomial ：目的変数が二値データであり（1: はい, 0: いいえ）、ロジスティック回帰を適用する、ということを指定する。

method=”brglmFit” ： バイアス減少型ロジスティック回帰。rare event（まれなアウトカム）や separation を避けるために使う。

上記ステータスを入力し、新たなロジスティック回帰モデル“ps_model”を作成します。

ここで一つ注意点があります。説明変数には今回、age, sex, BMI, Hb, PS (performance status)の5項目を入力しました。

この説明変数には明確な数の制限はありません。なので、必要と思われる説明変数は全て入れることができます。

ただ、IPTW法では下記に示すように、外れ値があるとps値が極端に大きくなってしまいます。

説明変数が多くなると、この極端な外れ値が生じるリスクも高まってしまいます。

入れる説明変数については十分に検討が必要です。

method=”brglmFit” は、Bias-reduced Generalized Linear Modelsを指します。

バイアスを減らすためのロジスティック回帰の方法です。

この文言を入れておくことで、エラーをだいぶ防ぐことができると思います。

glm()を用いた場合に、エラーが出ることがあります。

警告: glm.fit: アルゴリズムは収束しませんでした
警告: glm.fit: 数値的に 0 か 1 である確率が生じました

これは、「完全分離」によるエラーです。

もし仮に、drug_A = 1 の人が全員 sex = 1（例えば、女性）だったら…

→ glm() は「うまく係数が推定できない」

→ 結果として、無限大やNA になってしまう。ということになり、上記エラーが発生します。

また、 drug_A = 0 の人が全体の中で数人だけなど、かなり少ない場合、ロジスティック回帰の係数推定が不安定になりやすいという問題点があるようです。

このときにmethod=”brglmFit”を用いることで、「データが偏っているとき」や「希少なアウトカムがあるとき」に、より安定した推定ができる」という強みがあります！

現時点では、私はこのmethod=”brglmFit”はルーティンでいれても良いのでは？と思っています。

傾向スコアによる予測値（確率）の取得

# 傾向スコアによる予測値（確率）の取得
X_complete$ps <- predict(ps_model, type = "response")

predict(ps_model, type = “response”) は、作成したロジスティック回帰モデル ps_model を使って、各患者の drug_A を受ける確率（傾向スコア）を予測します。

type = “response” を指定することで、確率（0〜1の値）として出力されます。
X_complete$ps <-：データフレーム X_completeに新しい列 ps を追加し、各患者の傾向スコアを格納します。

これによって、データフレームX_completeにpropensity score（どの患者が drug_A を受ける可能性が高いか）を追加することができます！

IPTW法の重み計算

# IPTW法の重み計算
X_complete$iptw_weight <- ifelse(X_complete$drug_A == 1, 
                                  1 / X_complete$ps, 
                                  1 / (1 - X_complete$ps))

IPTW では、各個人に対して「治療を受ける確率（Propensity Score; PS）」の逆数を重みとして与えます。

・PS（Propensity Score） ＝ある患者が「治療」を受ける確率（0〜1）
・IPTW の重み
　　治療群（drug_A = 1）の重み = 1 / PS
　　非治療群（drug_A = 0）の重み = 1 / (1 – PS)

この調整によって、治療を受ける可能性が高い人と低い人の影響をバランスよく調整できます。

X_complete$iptw_weight → データ X_completeに新しい列 iptw_weightを追加。

ifelse(条件, 値1, 値2) → 条件に応じて異なる値を計算します。

X_complete$drug_A == 1（もしdrug_Aが”1″、つまり治療群の場合）→ 1 / X_complete$ps

X_complete$drug_A == 0（もしdrug_Aが”0″、つまり非治療群の場合）→ 1 / (1 – X_complete$ps)

このようにIPTWの重みを計算して、データフレームXに新たに作成したiptw_weightに保存されます。

このように、psまたは1-psの逆数を重み付けとします。

psは0から1の値を取ります。つまりpsが0か1に近くなるにつれて、psは極端に大きくなってしまうので、IPTW法においては特に注意が必要です！

ちなみに、このifelse関数は本当によく使います！Google検索すると沢山解説がありますので、是非確認して使いこなしていただければと思います。

重みの分布/NA除去

# 重みの分布/NA除去
summary(X_complete$iptw_weight)
X_complete <- X_complete[!is.na(X_complete$iptw_weight), ]

summary() → 重みの分布を確認。必ずしも必要ではないです…。

[!is.na(X_complete$iptw_weight), ]→NA のある行を削除（モデル不成立で ps が欠損したケースの除去）

重み付きサンプルデザイン（svydesign）

# 重み付きサンプルデザイン（svydesign）
design <- svydesign(ids = ~1, weights = ~iptw_weight, data = X_complete)

修正前、「survfit(Surv(survival_month, survival) ~ drug_A, weights = iptw_weight, data = X)」で、

IPTW法を適用したKaplan-Meier 生存曲線 (Kaplan-Meier Survival Curve) を作成するための生存分析モデル (survival model)を構築、と説明していました。

しかし、そもそもsurvdiff() は unweighted log-rank test しかサポートしていないため、iptw補正したp valueは反映されないと思われます。

そのため、修正前のプロトコルでは曲線自体は IPTW補正によるものだが、p-value はunweightedなデータ由来のp-valueと考えられます。

以下のスクリプトで、IPTW法による重み付けを考慮したp-valueをKaplan-meyer図に挿入していきます。

surveyパッケージの関数でサンプル設計を定義
ids = ~1 → 単純無作為抽出（クラスタなし）
weights = ~iptw_weight → IPTWを適用

Kaplan-Meier推定とlog-rank検定（重み付き）

# Kaplan-Meier推定とlog-rank検定（重み付き）
svykm_obj <- svykm(Surv(survival_month, survival) ~ drug_A, design=design)
svylogrank(Surv(survival_month, survival) ~ drug_A, design=design)

svykm() → 重み付きのKaplan-Meier曲線用オブジェクト作成

svylogrank() → 重み付き log-rank 検定

survfitを使ったKaplan-Meier作図用オブジェクト

# survfitを使ったKaplan-Meier作図用オブジェクト
km_fit_iptw <- survfit(Surv(survival_month, survival) ~ drug_A, 
                       weights = iptw_weight, data = X_complete)

survfit() は survey を通さず survival パッケージの関数

重みは weights = iptw_weight として指定可能

p値の抽出とテキスト化

# p値の抽出とテキスト化
logrank_test <- svylogrank(Surv(survival_month, survival) ~ drug_A, design=design)
p_value <- as.numeric(logrank_test[[2]]["p"])
p_text <- paste0("p = ", signif(p_value, 3))

log-rank 検定結果から p値を抽出し、"p = xxx" 形式の文字列として表示させる準備。

IPTW法によるKaplan-Meier曲線の描画

# IPTW法によるKaplan-Meier曲線の描画
ggsurvplot(
  km_fit_iptw, 
  conf.int = TRUE,
  risk.table = TRUE,
  title = "Kaplan-Meier Curve (IPTW adjusted)",
  legend.labs = c("No drug A", "Drug A"),
  xlab = "Time (months)",
  ylab = "Survival Probability",
  palette = c("#FC4E07", "#756BB1"),
  break.time.by = 12,
  pval = p_text
)

ggsurvplotを用いて、Kaplan-Meier曲線を描きます。

pval = p_text で、グラフ上に先ほど設定したp値を表示させます。

IPTW法であることをわかりやすくするために、title = “Kaplan-Meier Curve (IPTW adjusted)”にてタイトルをつけました。

実際の人数（計100名）と異なり、今回はだいぶ人数が増えた状態で解析されています。

これは、IPTW法を適用した場合、実際のサンプルサイズ（n数）とは異なる “有効サンプルサイズ（effective sample size, ESS）” で解析されるからのようです。

risk.table = FALSEとすれば、リスクテーブルが表示されなくなるので、ややっこしくなくて良いかもしれませんね！

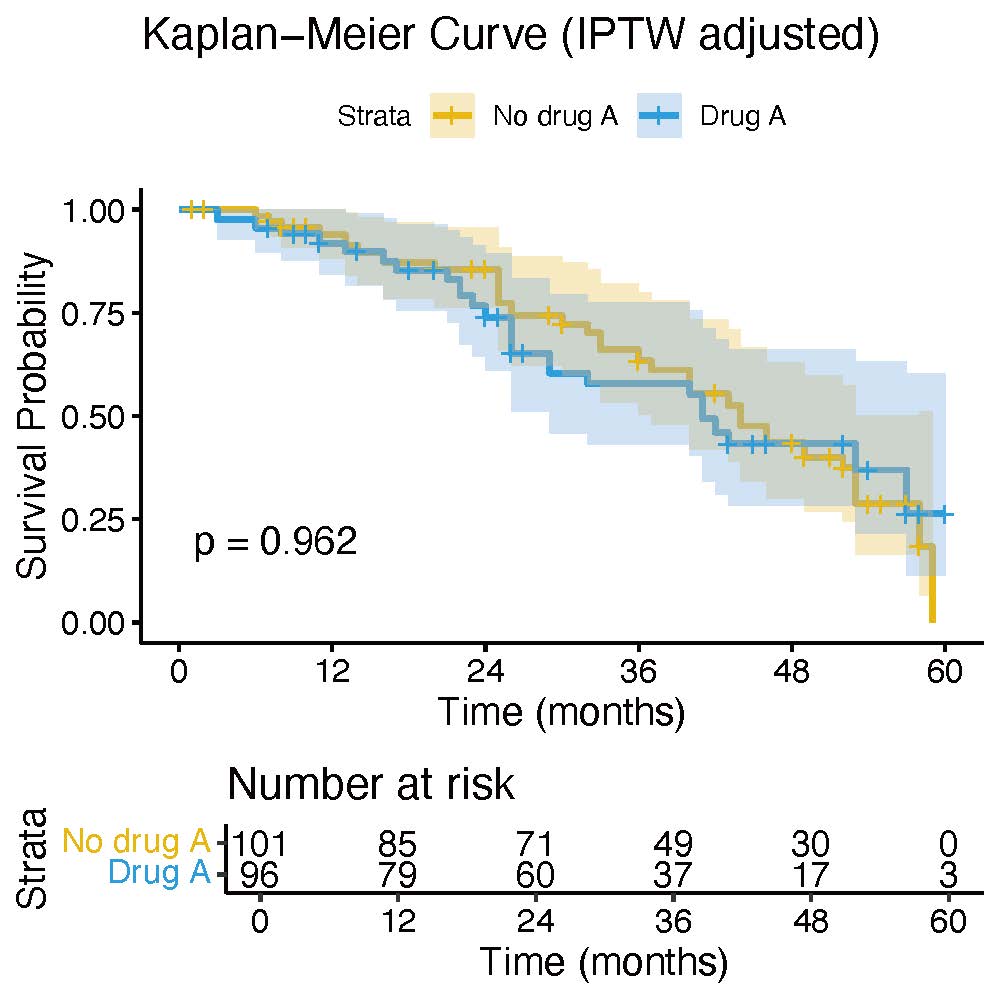
ChatGPTに尋ねたところ、IPTW法には以下のメリット・デメリットがあるようです。

✅ メリット

交絡因子を調整し、ランダム化試験に近い比較ができる
すべての共変量のバランスを同時に取れる（マッチング法より柔軟）

❌ デメリット

極端なPS（0 に近い or 1 に近い）があると、重みが大きくなりすぎる
適切なPS モデルを選ばないと、かえってバイアスが残る

応用編②：Overlap weighting法によるKaplan-Meier曲線の作成

Overlap weighting法は、IPTW法の欠点を補完する重み付け推定法として、最近注目されています。

IPTW法と同様、傾向スコア（Propensity Score, ps）を用いた重み付け推定の一つです。

治療効果を推定する際に、処置群（治療を受けた群）と対照群（治療を受けなかった群）の比較をより公平に行うための方法です。

特に、「オーバーラップ（重なり）」が大きい部分に重点を置くことで、より信頼性の高い推定を可能にします。従来のIPTW（Inverse Probability of Treatment Weighting）法と比べて、極端な重みがつきにくく、推定の安定性が向上する点が特徴です。

以下のブログに詳しく解説がなされており、参考にさせていただきました！

# 必要なパッケージを読み込み
library(tibble)
library(survival)
library(survminer)
library(brglm2)
library(survey)

# 欠損データの除去（complete cases）
X_complete <- X[complete.cases(X[, c("drug_A", "age", "sex", "BMI", "Hb", "PS")]), ]

# 傾向スコア（PS）モデルの構築
ps_model <- glm(drug_A ~ age + sex + BMI + Hb + PS,
                data = X_complete, family = binomial(), method = "brglmFit")

# 傾向スコアの取得
X_complete$ps <- predict(ps_model, type = "response")

# Overlap Weightingの計算
X_complete$ow_weight <- with(X_complete, ifelse(drug_A == 1, 1 - ps, ps))

# 欠損除外（念のため）
X_complete <- X_complete[!is.na(X_complete$ow_weight), ]

# 重み付きサンプルデザイン
design <- svydesign(ids = ~1, weights = ~ow_weight, data = X_complete)

# Kaplan-Meier推定とlog-rank検定（重み付き）
svykm_obj <- svykm(Surv(survival_month, survival) ~ drug_A, design = design)
logrank_test <- svylogrank(Surv(survival_month, survival) ~ drug_A, design = design)

# survfitを使ったKaplan-Meier作図用オブジェクト
km_fit_ow <- survfit(Surv(survival_month, survival) ~ drug_A, 
                     weights = ow_weight, data = X_complete)

# p値の抽出とテキスト化
p_value <- as.numeric(logrank_test[[2]]["p"])
p_text <- paste0("p = ", signif(p_value, 3))

# Overlap Weighting法によるKaplan-Meier曲線の描画
ggsurvplot(
  km_fit_ow, 
  conf.int = TRUE,
  risk.table = TRUE,
  title = "Kaplan-Meier Curve (Overlap Weighted)",
  legend.labs = c("No drug A", "Drug A"),
  xlab = "Time (months)",
  ylab = "Survival Probability",
  palette = c("#FC4E07", "#756BB1"),
  break.time.by = 12,
  pval = p_text
)

欠損データの除去/PSモデルの構築/傾向スコアの取得

# 欠損データの除去（complete cases）
X_complete <- X[complete.cases(X[, c("drug_A", "age", "sex", "BMI", "Hb", "PS")]), ]

# 傾向スコア（PS）モデルの構築
ps_model <- glm(drug_A ~ age + sex + BMI + Hb + PS,
                data = X_complete, family = binomial(), method = "brglmFit")

# 傾向スコアの取得
X_complete$ps <- predict(ps_model, type = "response")

ここの部分はIPTW法と全く同じですね。

Overlap Weightingの計算

# Overlap Weightingの計算
X_complete$ow_weight <- with(X_complete, ifelse(drug_A == 1, 1 - ps, ps))

# 欠損除外（念のため）
X_complete <- X_complete[!is.na(X_complete$ow_weight), ]

Overlap Weighting法では、各個体に以下のような重み（weight）を付けます：

・PS（Propensity Score） ＝ある患者が「治療」を受ける確率（0〜1）
・Overlap Weightingの重み
　処置群（Treatment group）:1−PS
　対照群（Control group）: PS

IPTWでは、PSが0または1に近いと極端に大きな重みがつくことがあります（不安定）。

Overlap Weightingでは、PSが0または1に近い個体の重みが小さくなるため、安定した推定が可能です。

PSが0.2～0.8程度の中間層に重点を置くことで、バランスが取りやすくなると言われています。

重み付きサンプルデザイン〜p値の抽出とテキスト化

# 重み付きサンプルデザイン
design <- svydesign(ids = ~1, weights = ~ow_weight, data = X_complete)

# Kaplan-Meier推定とlog-rank検定（重み付き）
svykm_obj <- svykm(Surv(survival_month, survival) ~ drug_A, design = design)
logrank_test <- svylogrank(Surv(survival_month, survival) ~ drug_A, design = design)

# survfitを使ったKaplan-Meier作図用オブジェクト
km_fit_ow <- survfit(Surv(survival_month, survival) ~ drug_A, 
                     weights = ow_weight, data = X_complete)

# p値の抽出とテキスト化
p_value <- as.numeric(logrank_test[[2]]["p"])
p_text <- paste0("p = ", signif(p_value, 3))

この部分も、基本的にはIPTW法と同じです。

Overlap weighting法によるKaplan-Meier曲線の描画

# Overlap Weighting法によるKaplan-Meier曲線の描画
ggsurvplot(
  km_fit_ow, 
  conf.int = TRUE,
  risk.table = TRUE,
  title = "Kaplan-Meier Curve (Overlap Weighted)",
  legend.labs = c("No drug A", "Drug A"),
  xlab = "Time (months)",
  ylab = "Survival Probability",
  palette = c("#FC4E07", "#756BB1"),
  break.time.by = 12,
  pval = p_text
)

ggsurvplotを用いて、Kaplan-Meier曲線を描きます。

ここも、IPTW法とほぼ一緒です。km_fit_iptwをkm_fit_owに置き換えるだけです。

Overlap Weighting法を適用した場合も、実際のサンプルサイズ（n数）とは異なる “有効サンプルサイズ（effective sample size, ESS）” で解析されるため、実際のサンプルサイズとは異なっていることに注意してください。

リスクテーブルを消去したい場合は、risk.table = FALSEとしましょう。

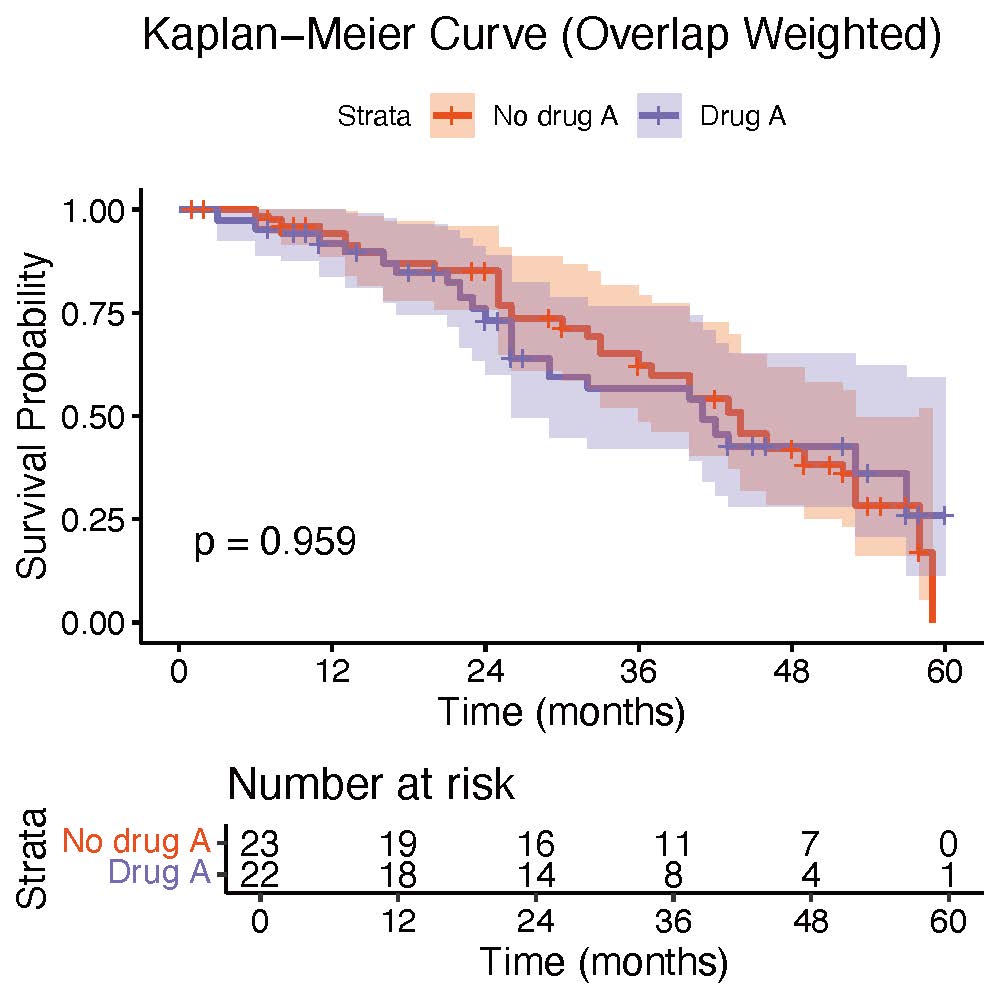
このように、上記の流れで解析をすれば、通常のKaplan-Meier法だけでなくIPTW法も、Overlap Weighting法も、解析対象に応じて柔軟に変更することが可能で便利です！

COX比例ハザードモデル

蛇足ですが、この架空データベースを用いてCox比例ハザードモデルもIPTW法・overlap weight法にて行うことができます。

# IPTW法でのCox比例ハザードモデル
cox_iptw <- coxph(Surv(survival_month, survival) ~ drug_A + age + sex + BMI + Hb + PS, weights = X_complete$iptw_weight, data = X_complete)
summary(cox_iptw) #結果の表示

# Overlap weighting法でのCox比例ハザードモデル
cox_ow <- coxph(Surv(survival_month, survival) ~ drug_A + age + sex + BMI + Hb + PS, weights = X_complete$ow_weight, data = X_complete)
summary(cox_ow) #結果の表示

例えばIPTW法におけるCOX比例ハザードモデルの結果は、下記のように表示されます。

> summary(cox_iptw) #結果の表示
Call:
coxph(formula = Surv(survival_month, survival) ~ drug_A + age + 
    sex + BMI + Hb + PS, data = X_complete, weights = X_complete$iptw_weight)

  n= 100, number of events= 54 

            coef exp(coef)  se(coef) robust se      z Pr(>|z|)  
drug_A  0.058021  1.059737  0.201502  0.288991  0.201   0.8409  
age     0.018178  1.018344  0.007917  0.010978  1.656   0.0977 .
sex    -0.436405  0.646356  0.210564  0.305054 -1.431   0.1526  
BMI     0.008084  1.008117  0.019899  0.032106  0.252   0.8012  
Hb     -0.054165  0.947276  0.044870  0.062236 -0.870   0.3841  
PS     -0.035269  0.965346  0.073789  0.099554 -0.354   0.7231  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

       exp(coef) exp(-coef) lower .95 upper .95
drug_A    1.0597     0.9436    0.6015     1.867
age       1.0183     0.9820    0.9967     1.040
sex       0.6464     1.5471    0.3555     1.175
BMI       1.0081     0.9919    0.9466     1.074
Hb        0.9473     1.0557    0.8385     1.070
PS        0.9653     1.0359    0.7942     1.173

Concordance= 0.562  (se = 0.044 )
Likelihood ratio test= 11.46  on 6 df,   p=0.08
Wald test            = 8.71  on 6 df,   p=0.2
Score (logrank) test = 11.32  on 6 df,   p=0.08,   Robust = 7.09  p=0.3

  (Note: the likelihood ratio and score tests assume independence of
     observations within a cluster, the Wald and robust score tests do not).

さて、Cox比例ハザードモデルにおいて、そもそもIPTW法やOverlap Weighting法を適用することに、一体何の意味があるのでしょうか？

実際にGoogle検索してみると、ちらほら「IPTW Cox回帰」について解説されているサイトをみかけました。

しかし、その意義についてはあまり詳述されていません…。

ということで、ChatGPTさんに聞いてみました（笑）

📌 Cox比例ハザードモデルにIPTW法やOverlap Weighting法を適用する意義

Cox比例ハザードモデルによる多変量解析 では、治療（例: drug_A）と生存期間の関係を評価する際、交絡因子（年齢・性別・BMI など）の影響を調整する必要があります。
この調整方法として、IPTW（Inverse Probability of Treatment Weighting）法や Overlap Weighting（OW）法を適用することが可能です。

1️⃣ IPTW法を適用する意義

IPTW法では、各患者の Propensity Score（PS; 治療を受ける確率）を用いて重み付けを行い、疑似的に無作為化比較試験（RCT）に近づけることを目指します。

✅ 交絡因子を調整し、治療効果のバイアスを減らす
✅ 「治療を受ける確率が高い患者」と「治療を受ける確率が低い患者」のバランスを取る
✅ RCTのような「治療の割り付けがランダムな状況」に近づける

2️⃣ Overlap Weighting（OW）法を適用する意義

Overlap Weighting法は、Propensity Scoreが0.5に近い患者（治療と非治療のどちらにも属する可能性が高い患者）に重点を置いて解析する方法 です。

✅ 治療群と非治療群の「共通サポート領域（overlap region）」を重視する
✅ 極端な PS を持つ患者（0 or 1に近い患者）を減らし、外れ値の影響を抑える
✅ バランスの取れた母集団における治療効果を推定できる

とのこと。

意義はありそうですね。特にIPTW法を用いることで、後ろ向き試験であってもRCTのような均一な患者背景に近づけた上で、Cox比例ハザードモデルを適用できる、というメリットがありそうです。

さいごに

# スクリプト全景

# 必要なパッケージを読み込み
library(tibble)
library(survival)
library(survminer)
library(brglm2)
library(survey)

# 欠損データの除去（complete cases）
X_complete <- X[complete.cases(X[, c("drug_A", "age", "sex","BMI",
                                     "Hb", "PS")]), ]

# Propensity Score (PS) モデルの構築
ps_model <- glm(drug_A ~ age + sex + BMI + Hb + PS,
                data = X_complete, family = binomial(), method="brglmFit")

# 傾向スコアによる予測値（確率）の取得
X_complete$ps <- predict(ps_model, type = "response")

# IPTW法
X_complete$iptw_weight <- ifelse(X_complete$drug_A == 1, 
                                  1 / X_complete$ps, 
                                  1 / (1 - X_complete$ps))
summary(X_complete$iptw_weight)
X_complete <- X_complete[!is.na(X_complete$iptw_weight), ]
design <- svydesign(ids = ~1, weights = ~iptw_weight, data = X_complete)
svykm_obj <- svykm(Surv(survival_month, survival) ~ drug_A, design=design)
svylogrank(Surv(survival_month, survival) ~ drug_A, design=design)
km_fit_iptw <- survfit(Surv(survival_month, survival) ~ drug_A, 
                       weights = iptw_weight, data = X_complete)
logrank_test <- svylogrank(Surv(survival_month, survival) ~ drug_A, design=design)
p_value <- as.numeric(logrank_test[[2]]["p"])
p_text <- paste0("p = ", signif(p_value, 3))
ggsurvplot(
  km_fit_iptw, 
  conf.int = TRUE,
  risk.table = TRUE,
  title = "Kaplan-Meier Curve (IPTW adjusted)",
  legend.labs = c("No drug A", "Drug A"),
  xlab = "Time (months)",
  ylab = "Recurrent Probability",
  palette = c("#FC4E07", "#756BB1"),
  break.time.by = 12,
  pval = p_text
)

# Overlap Weighting法
X_complete$ow_weight <- with(X_complete, ifelse(drug_A == 1, 1 - ps, ps))
X_complete <- X_complete[!is.na(X_complete$ow_weight), ]
design <- svydesign(ids = ~1, weights = ~ow_weight, data = X_complete)
svykm_obj <- svykm(Surv(survival_month, survival) ~ drug_A, design = design)
logrank_test <- svylogrank(Surv(survival_month, survival) ~ drug_A, design = design)
km_fit_ow <- survfit(Surv(survival_month, survival) ~ drug_A, 
                     weights = ow_weight, data = X_complete)
p_value <- as.numeric(logrank_test[[2]]["p"])
p_text <- paste0("p = ", signif(p_value, 3))
ggsurvplot(
  km_fit_ow, 
  conf.int = TRUE,
  risk.table = TRUE,
  title = "Kaplan-Meier Curve (Overlap Weighted)",
  legend.labs = c("No drug A", "Drug A"),
  xlab = "Time (months)",
  ylab = "Survival Probability",
  palette = c("#FC4E07", "#756BB1"),
  break.time.by = 12,
  pval = p_text
)

ちなみに、サムネイルはAdobe Fireflyで作ってみました。

参考にしたブログ・HP

統計ER①（https://toukeier.hatenablog.com/entry/how-to-draw-IPTW-KM-curve）
統計ER②（https://toukeier.hatenablog.com/entry/2019/08/06/221320）
統計ER③（https://best-biostatistics.com/toukei-er/entry/iptw-cox-regression-in-r/）
ねこすたっと（https://necostat.hatenablog.jp/?page=1632778023）
統計学入門一歩先へ（https://mstour.hatenablog.com/entry/2022/08/06/125817）

イラスト・画像元

Adobe firefly: https://firefly.adobe.com/?media=featured